Introduction to Support Vector Machines
1.间隔最大化
1.1 关于线性分类器的选择的思考
SVM本源也是一个线性分类器;
对于线性分类器,有一个需要认识到的事实(证明略):
若样本集是线性可分的,那么存在一条直线可以将样本正确分类;
若存在一条直线可以将样本正确分类,则存在无数条直线可以将样本正确分类。
问题出现。面对无数条能够正确分类训练样本的直线,我们如何选取最优的一条?或者说是否有一个评价分类器优劣的指标?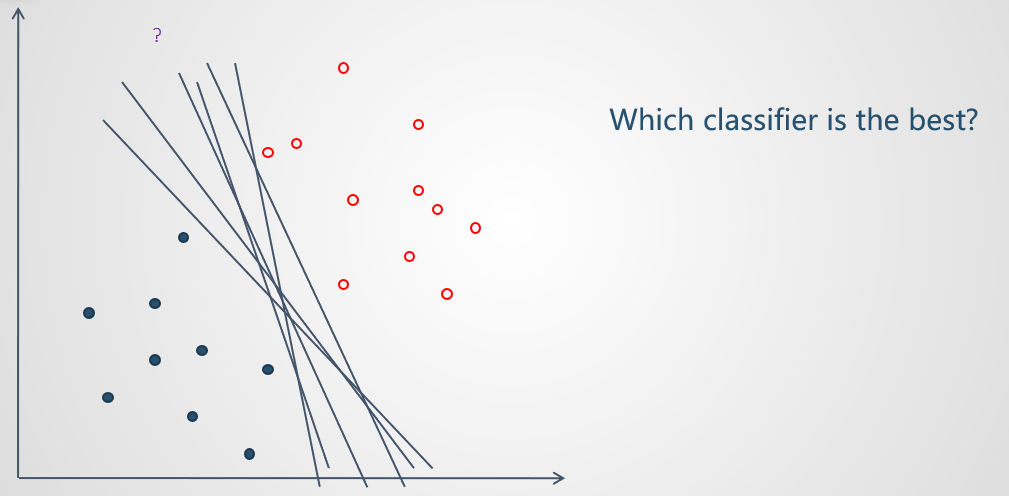
1.2 margin 的引入
为了进一步评估分类器的表现,我们引入了新的指标 margin;
可以这样形象地理解:分类器在没有样本点的空间内可以移动的最大范围;
我们对于一个良好的分类器有这样的期待,它的 margin 越大越好,因为这样的分类器对于训练样本的局部扰动的容忍性较好(fault tolerance);
试想走在一条险路上,两边都是悬崖,那么我们通过时会尽量走在中间,这样稍有不慎也不会掉下去,比较有安全感。
为了简化表达式,可以令 margin 的两个边界分别为(涉及到函数间隔与几何间隔,略):
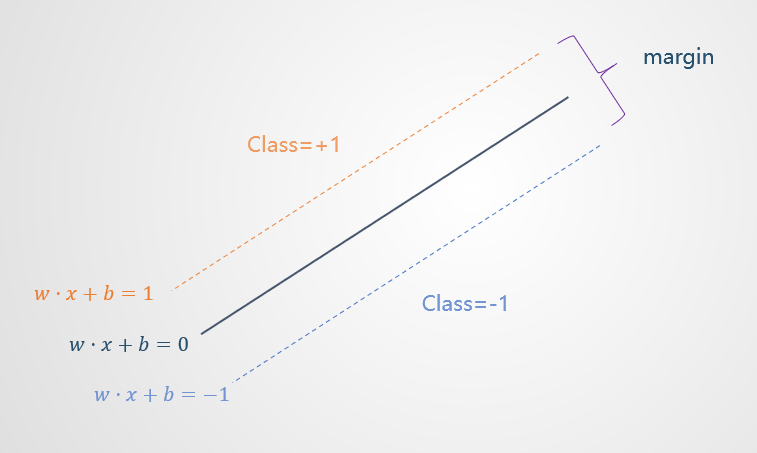
于是, margin 可写作:
1.3 问题的形式化表达
Two step:
- 正确分类样本(约束)
- 最大化间隔(优化)
2.拉格朗日乘子法
2.1 优化问题
Minimize:
Subject to:
这里将优化目标函数作了细微的变化,转换成了最小化向量 w 的内积的形式;
有两个目的:
- 方便对 w 求导;
- 便利于后面引入核函数(涉及到大量的空间中向量的内积的运算)
2.2 拉格朗日函数
写出拉格朗日函数,将含有分类器参数 w 和 b 的约束条件蕴含进优化函数:
2.3 原问题与对偶问题
原问题转换为拉格朗日函数的极小极大问题(证明略):
对偶问题为极大极小问题:
一般情况下,极小极大问题是不小于其对偶问题(极大极小问题)的;
这种情况称之为弱对偶性(Weak Duality):
通俗理解:凤尾与鸡头
当满足特定条件时,极小极大问题可与其对偶问题等价,即满足强对偶性(Strong Duality),这个特定条件是KKT(Karush-Kuhn-Tucker)条件;
针对本优化问题(包含不等式约束条件的优化问题),KKT条件如下:
其中第2个式子称之为松弛互补条件;
其乘积为0的两个因子分别在第3、4式子作出约束;
- 当4式 “=” 成立时,对3式无约束;
- 当4式 “<” 成立时,3式参数取0;
可理解为参数仅作用于支持向量(边界上的样本点,满足4式的”=”条件)
满足了KKT条件之后,接下来就可以通过求解对偶问题实现原问题的求解。
2.4 对偶问题(极大极小问题)的求解
首先,求解内层的极小化问题:
分别对 w 和 b 求偏导为0:
将结果代回拉格朗日函数,得到极小结果:
然后,求解外层的极大化问题:
变换符号,转换成极小化形式:
从以上的极小化问题求解得到参数结果 α*, 可得原问题参数 w* 和 b* 的解:
从而,分类决策函数可写作:
3.软间隔SVM
在前面的讨论中,我们一直默认着一个前提,即训练数据是线性可分的,然而这仅仅是理想情况;
现实情况往往要复杂得多,要么数据勉强线性可分但存在噪点,要么就是完全线性不可分;
针对有噪点的情况,提出了软间隔的概念;
所谓软间隔,其实就是放宽了约束条件;
比如说原先考试都是60分为及格线,但是同学们的学习效果太差,如果按照60分的标准,总有人不及格,那么这样,如果再加上10分,能够达到标准,就算及格;
3.1 松弛变量
形式化地,引入了 $\xi$ 这一松弛变量,放宽了约束条件:
由于放宽了约束条件,优化函数需要加入一个惩罚量:
其中 $ C > 0 $ 称之为惩罚参数,C越小时对误分类惩罚越小,越大时对误分类的惩罚越大;
当C取正无穷时,就变成了硬间隔优化;
实际应用时需要选取合理的C,C太小容易欠拟合,太大容易过拟合
3.2 软间隔SVM求解
求解过程与线性可分的硬间隔情况相同,过程略;
求得结果如下:
不难发现与硬间隔的情况殊途同归,形式几乎一致,
仅仅是多了个 $ \alpha_{i} \leq C $ 的约束条件
4.非线性SVM与核技巧
需要明确的是,软间隔不是用来处理线性不可分问题的,它只能在存在噪点的情况下做一些放宽约束的处理;
真正遇到线性不可分问题的时候,需要换一个思路了
4.1 两个例子
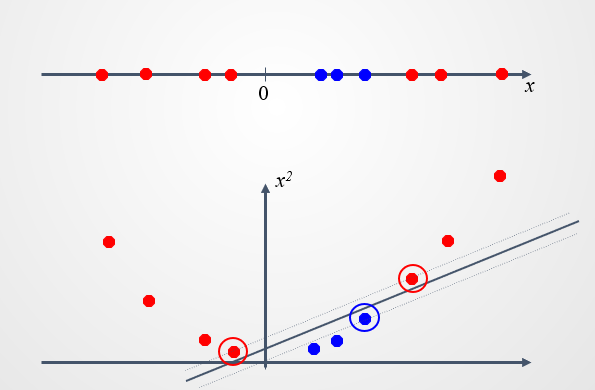
在上面这幅图中,红色点和蓝色点在一维坐标中是线性不可分的;
而当将其投影到二维空间中,发现可以用一条直线完美分开;
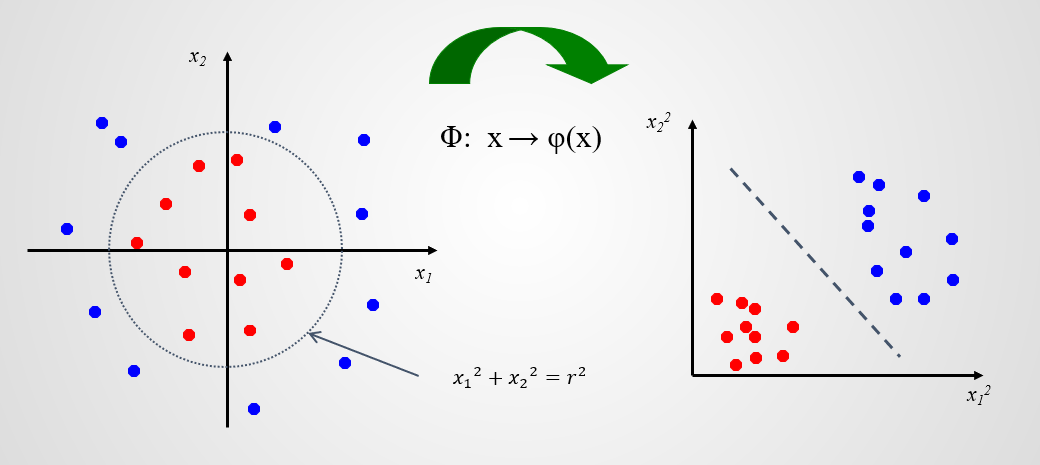
再来看这个例子,红色样本分布在中间,蓝色样本分布在外围;
凭观察不难发现可以用一个圆将两种样本分开;
也可以做一个映射,投影到 $ x{1}^{2} - x{2}^{2} $ 空间中;
则又可以用一条直线将样本分开;
这两个例子给出一个启示:
原始问题很复杂,至少是线性分类器无法解决的,把它映射到更高维度的空间,就很有可能豁然开朗了;
这就是SVM非常核心的一个思想,不是说去生成一个多么负责的分类器模型,而是对问题进行转换,转换成一个更加容易去解决的。
4.2 映射的设计
那么到底怎么去设计这个低维到高维的映射呢?
其实没有必要针对每一个问题单独设计;
有那么几种固定的映射方法;
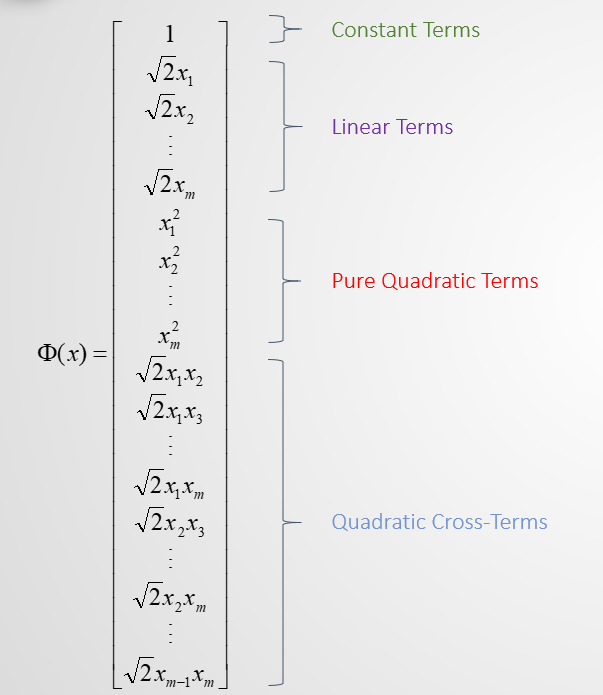
这是其中一种映射,其中包含常数项、线性项、二次项、交叉项;
如果原空间是 $ m $ 维的,那么映射后的空间就会达到 $ m^{2} $ 维,可能会是非常高的维度;
这也许与通常的思路有点相悖;
降维是我们经常处理的工作,在这里,却把维度提高,大大增加了计算复杂度;
其实这其中还有精妙的设计!
4.3 核技巧
在SVM中,向量的内积是十分核心的计算操作;
这里,我们尝试着将两个已被映射到高维空间的向量作内积运算:
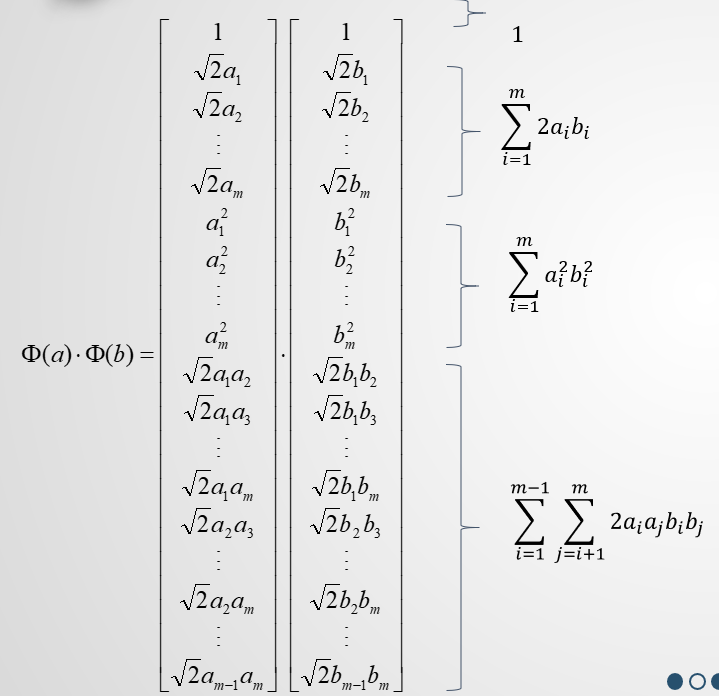
得到高维空间的内积结果:
再尝试着在低维空间中计算这样一个式子:
惊喜地发现,低维空间的计算结果正好与高维空间的计算结果一致。
这意味着,我们可以用低维空间的运算等价于高维空间的运算,大大减小了计算量。
所以我们可以定义这样一个函数,在$m$维空间做运算,其实际效果等价于高维空间的运算。
这样的函数称之为核函数,这样的方法称之为核方法(Kernal Trick)。
核方法利用了高维空间数据非常好分的优点,又巧妙地避开了高维空间计算量大的缺点。是SVM思想的精髓所在。
4.4 常用的核函数
下面例举几个常见的核函数:
- Polynomial:
- Gaussian:
- Hyperbolic Tangent:
5.实验
在学习了SVM的理论知识后,为了更好地理解和应用SVM,我们还使用了scikit-learn机器学习包来进行SVM模型的训练和部署。
环境:Python 3.8.5,scikit-learn 0.23.2,Ubuntu 20.04
binary_classification.py:
基于Iris数据集中Setosa和Versicolour的数据作二分类,特征使用萼片(sepal)的宽度和长度,目标是分成Setosa和Versicolour两个类别。
关键代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14# 150x4 iris datasets
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
# only select Setosa and Versicolour
# to conduct binary classfication
selected = (y == 0) | (y == 1)
X = X[selected]
y = y[selected]
# SVM Classifier model
bi_clf = SVC(kernel="linear", C=float("inf"))
bi_clf.fit(X, y)
以下是模型拟合后的示意图:(绿色高亮的点即是支持向量)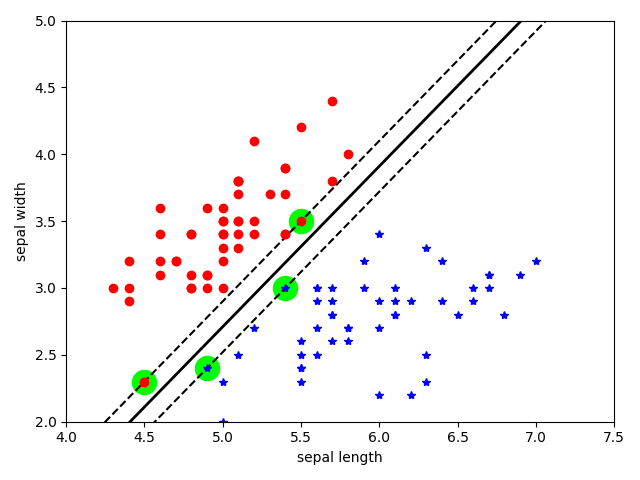
multi_classification.py:
基于Iris数据集作多分类,一对一策略。特征仍是二维的,仍使用萼片(sepal)的宽度和长度,目标则是分成Setosa,Versicolour和Virginica三个类别。
关键代码与binary_classification.py类似:1
2
3
4# SVM Classifier model
# one-versus-one strategy
multi_clf = SVC(kernel="linear", decision_function_shape='ovo')
multi_clf.fit(X, y)
以下是模型拟合后的示意图: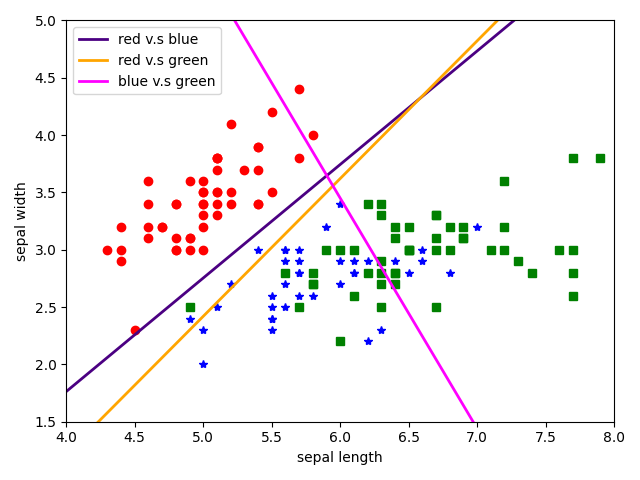
rbf_kernel.py:
RBF核函数解决线性可分问题。使用了多一维的特征-花瓣(petal)的长度,目标是Versicolour和Virginica两个类别。
关键代码:(需要额外使用mplot3d库来绘制三维图像)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from mpl_toolkits import mplot3d
...
# 150x4 iris datasets
iris = datasets.load_iris()
X = iris.data[:, :3]
y = iris.target
selected = (y == 1) | (y == 2)
X = X[selected]
y = y[selected]
ax = plt.axes(projection='3d')
ax.plot3D(X[:, 0][y==1], X[:, 1][y==1], X[:, 2][y==1], "ro")
ax.plot3D(X[:, 0][y==2], X[:, 1][y==2], X[:, 2][y==2], "bs")
ax.set_xlabel("sepal length")
ax.set_ylabel("sepal width")
ax.set_zlabel("petal length")
# SVM Classifier model
rbf_clf = SVC(kernel="rbf")
rbf_clf.fit(X, y)
以下是模型拟合后的示意图: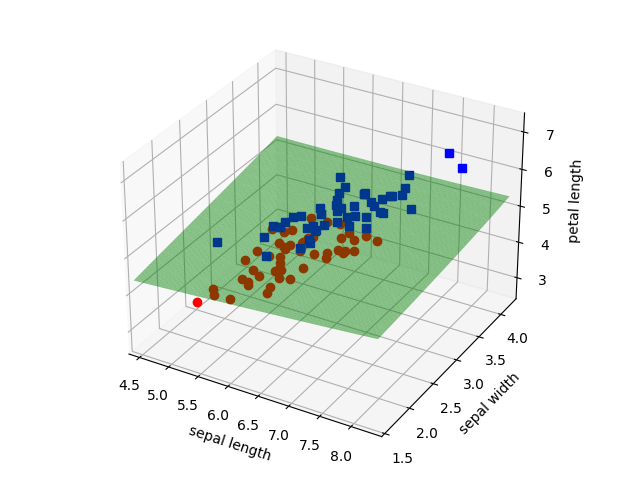
non_linear.py:
使用RBF核函数,训练拟合线性不可分的异或函数。
关键代码:1
2
3
4
5
6
7# generate random xor datasets
X = np.random.randn(150, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
# SVM Classifier model
non_linear_clf = SVC(kernel="rbf")
non_linear_clf.fit(X, y)
以下是模型拟合后的示意图: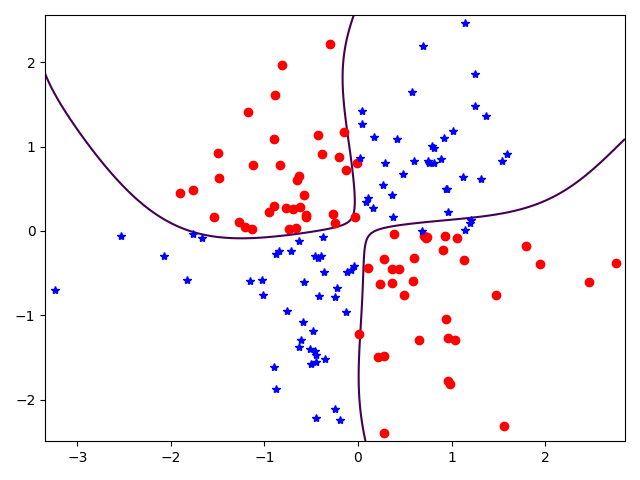
6.参考文献
[1] CristianintNello. An introduction to support vector machines and other kernel-based learning methods[J]. 2000.
[2] 李航. 统计学习方法[M]. 清华大学出版社, 2012.
[3] Peter Harrington, 李锐. 机器学习实战 : Machine learning in action[M]. 人民邮电出版社, 2013.
[4] 吴建鑫. 模式识别. 机械工业出版社, 2020.